 Оценка 720
[+1/-0]
Оценка 720
[+1/-0]

 Оценить
Оценить 





 Оценка 720
[+1/-0] Оценка 720
[+1/-0]
  Оценить Оценить       
|
| Просто конечные автоматы Добавляем недетерминированность … и эпсилон-переходы И почему это круто Реализация методом «в лоб» Реализация преобразованием в ДКА Заключение |  |
Подвёл ты меня, Боролгин. А ведь я все деньги на тебя поставил. .. <тут Боролгин сокрушается> .. Не горюй, Боролгин. Я ещё и на орков поставил. Арагорн в переводе Гоблина
Недетерминированные конечные автоматы – одна из моделей, используемых в теории вычислений. Вряд ли всё это когда-нибудь пригодится вам «по жизни»… но, чёрт возьми, математика – это интересно! Во всяком случае, для меня. А если уж она хоть как-то с программированием связана, то интересна вдвойне.
Я не претендую на математическую строгость, получилось что-то типа «популярной математики для чайников»… Но надо же с чего-то начинать. А причём здесь орки – поймёте по ходу дела :)
Скорее всего, все более-менее знают, что такое конечные автоматы. Проблема в том, что я, например, знаю три варианта: конечные автоматы Мура, конечные автоматы Мили и «просто» конечные автоматы. Поскольку дальше нам потребуется вполне конкретное определение, имеет смысл ввести его здесь.
Итак, детерминированным конечным автоматом (ДКА) называется устройство, описываемое следующими параметрами:
И функционирующие следующим образом:
| ПРИМЕЧАНИЕ Возможно, более простым вам покажется следующее определение: детерминированным конечным автоматом называется такой автомат, в котором при любой данной последовательности входных символов существует лишь одно состояние, в которое автомат может перейти из текущего. – прим.ред. |
Работа ДКА заключается в распознавании цепочек символов, принадлежащих множеству Σ. Если, обработав цепочку, автомат оказался в допускающем состоянии, то цепочка считается допустимой, если нет, то нет. Таким образом, ДКА задаёт некоторый язык – множество допускаемых им цепочек, алфавит этого языка – множество Σ.
| ПРИМЕЧАНИЕ Это определение конечного автомата используется в теории вычислений. Автоматы Мура и Мили используются, в основном, при проектировании цифровой аппаратуры. |
Конечные автоматы удобно изображать графически. На рисунке 1 приведён несложный ДКА, допускающий цепочки из 0 и 1, заканчивающиеся символом 0. Начальное состояние помечено входящей в него стрелочкой (да, этот здоровенный треугольник в душе – стрелочка), допускающее (в данном случае оно одно) – двойным кружком.

Рисунок 1. Простой детерминированный конечный автомат.
Второй вариант изображения автоматов – таблица переходов.
| 0 | 1 | ||
|---|---|---|---|
| -> | q0 | q1 | q0 |
| * | q1 | q1 | q0 |
По горизонтали отложены символы входного алфавита, по вертикали – состояния, начальное состояние отмечено стрелочкой, а допускающие – звёздочками. Этот способ изображения менее нагляден, и приведён только в качестве примера, использовать его «для дела» я не буду.
Определение недетерминированного конечного автомата (НКА) практически полностью повторяет приведённое выше определение ДКА. Отличий всего два:
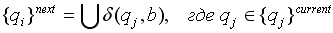
НКА тоже распознаёт цепочки символов, цепочка считается допустимой, если после её обработки множество состояний, в котором оказался автомат, содержит хотя бы одно допускающее. Таким образом, НКА также задаёт некоторый язык.
На рисунке 2 изображён простой НКА, допускающий цепочки из 0 и 1, заканчивающиеся на 00.
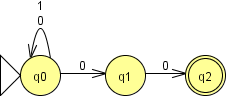
Рисунок 2. Простой недетерминированный конечный автомат.
Этот же автомат в виде таблицы:
| 0 | 1 | ||
|---|---|---|---|
| -> | q0 | {q0, q1} | {q0} |
| q1 | {q2} | Ø | |
| * | q2 | Ø | Ø |
Разберёмся, как он работает.
Допустим, на вход автомату поступила цепочка «100100».
| До | Вход | Описание | После |
|---|---|---|---|
| Автомат начинает работу в множестве состояний {q0} | {q0} | ||
| {q0} | 1 | Из состояния q0 по символу 1 существует только один переход, в q0 же. | {q0} |
| {q0} | 0 | Из состояния q0 по символу 0 существует два перехода, в q0 и в q1. | {q0, q1} |
| {q0, q1} | 0 | Из состояния q0 по символу 0 существует два перехода, в q0 и в q1, из состояния q1 – один переход, в q2. Поскольку автомат находится в двух состояниях, множества объединяются. | {q0, q1, q2} |
| {q0, q1, q2} | 1 | Автомат находится в трёх состояниях, но из q1 и из q2 не существует переходов по символу 1 (т.е. значение функции перехода из этих состояний по входному символу 1 – пустое множество). В итоге остаётся только q0. | {q0} |
| {q0} | 0 | И т.д. | {q0, q1} |
| {q0, q1} | 0 | И т.п. Так как в получившемся множестве состояний есть q2 – допускающее состояние, автомат признаёт цепочку корректной. | {q0, q1, q2} |
Менее формальное, но немного более наглядное представление обработки той же цепочки тем же автоматом изображено на рисунке 3.
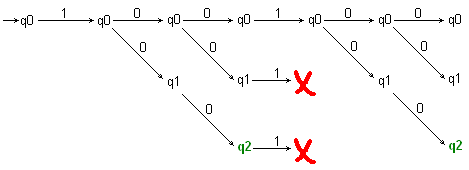
Рисунок 3. Обработка цепочки 100100
В данном случае мы несколько удаляемся от определения НКА (множества состояний не представлены так явно). Картинка основана на следующей идее: каждый раз, когда по входному символу возможен переход в несколько состояний, порождается новая ветка вычислений, когда переходов нет – ветка «засыхает». Если хоть одна из «живых» веток ведёт в допускающее состояние – цепочка допущена.
В общем, подходы дают аналогичные результаты, за исключением одной мелочи. Слегка изменённый НКА, изображённый на рисунке 4, допускает любую цепочку символов {0, 1}, содержащую два нуля подряд. Если каждый раз честно порождать новую ветку, то при обработке цепочки «1001001….» получится дерево, изображённое на рисунке 5. Понятно, что две нижние ветки полностью совпадают (они представляют одинаковые состояния автомата, получают одинаковые входы, значит и результаты будут одинаковые), более того, каждый раз, когда в цепочке будет встречаться 00, будет порождаться ещё одна точно такая же ветка.
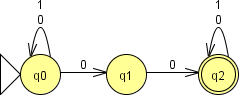
Рисунок 4. Немного изменённый НКА
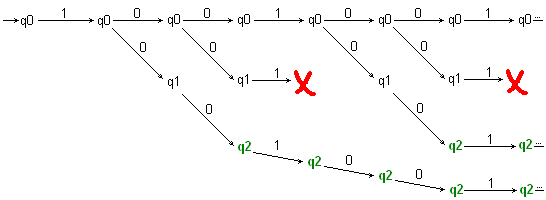
Рисунок 5. Обработка цепочки 1001001.
Можно добавить слияние одинаковых веток, но это уменьшит наглядность. В подходе, основанном на множествах, слияние происходит автоматически – множество не может содержать два одинаковых элемента.
Наименее формальный подход к описанию работы НКА основан на том, что он «угадывает». Вернёмся к автомату на рисунке 2 и цепочке «100100».
| До | Вход | Описание | После |
|---|---|---|---|
| Автомат начинает работу в состоянии {q0} | q0 | ||
| q0 | 1 | Из состояния q0 по символу 1 существует только один переход, в q0 же. | q0 |
| q0 | 0 | Из состояния q0 по символу 0 существует два перехода, в q0 и в q1. Но! Автоматугадал, что эта последовательность нулей – ещё не конец цепочки. Поэтому остаёмся в q0. | q0 |
| q0 | 0 | И т.д. | q0 |
| q0 | 1 | И т.п. | q0 |
| q0 | 0 | А вот теперь автоматугадал, что это завершение, и что следующим входным символом тоже будет 0 (иначе нет смысла переходить в q1 – из него нет переходов по 1). Переход в q1 | q1 |
| q1 | 0 | Из q1 только один переход – в q2. Цепочка допущена. | q2 |
То есть, фактически, мы взяли дерево из подхода №2, и обрезали все ветки, кроме одной – наиболее успешной.
Небольшое полезное расширение стандартного НКА – ε-НКА, или НКА с эпсилон-переходами.
«Эпсилон-переходом» называется переход между состояниями, который может быть выполнен автоматом «просто так», без входного символа. На графах и в таблицах такие переходы обычно помечаются символом ε.
| ПРИМЕЧАНИЕ В замечательной программе JFLAP, скриншоты из которой используются в качестве рисунков, ε-переходы почему-то обозначаются символом λ, но я нашёл в себе силы поправить картинки. |
На рисунке 6 изображён пример ε-НКА.
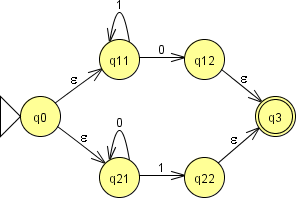
Рисунок 6. НКА с ε-переходами.
Как это ни удивительно, но на этом немного странном примере продемонстрировано одно из наиболее полезных свойств ε-переходов – возможность простого объединения нескольких автоматов в один. В данном случае объединяемыми автоматами являются НКА, изображённые на рисунке 7, а результирующий автомат допускает цепочки, допустимые хотя бы одним из них.
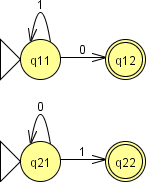
Рисунок 7. Составные части автомата, показанного на рисунке 6.
Кроме того, обратите внимание, что никаких дополнительных ограничений на ε-переходы не накладывается. То есть:
В общем, граф/таблица переходов автомата выглядят так, как будто во входном алфавите появился ещё один символ – ε, а его работа так, будто в любом месте обрабатываемой цепочки (в начале, в конце, между символами) находится произвольное количество этих символов. При этом для каждого состояния есть как минимум один переход по ε – в себя.
Введём понятие ε-замыкание.
Функцию eclose можно определить так:
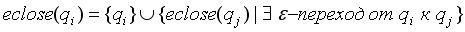
А теперь мы можем строго определить функционирование ε-НКА.
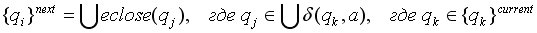
Допустим, вам нужен автомат, распознающий двоичные, десятичные и шестнадцатеричные числа в стандартном ассемблерном формате (я понимаю, что такие ситуации происходят в вашей жизни нечасто, но я и так сломал голову в поисках не слишком искусственного примера). То есть, допустимая строчка должна описываться одним из следующих утверждений:
Решение показано на рисунке 8.
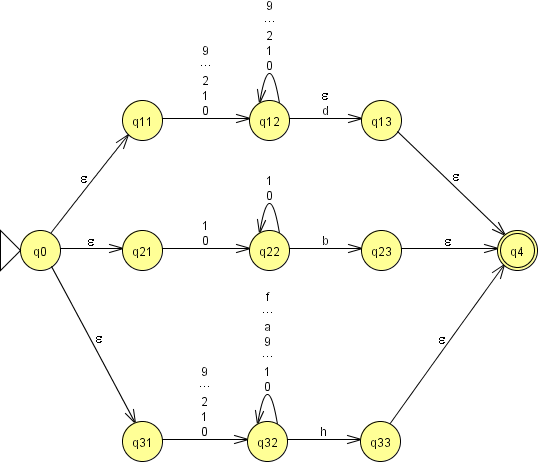
Рисунок 8. ε-НКА, распознающий числа в ассемблерном формате
Что в первую очередь радует в этом конечном автомате – то, что он понятен и изменяем. Посмотрев на граф, можно практически сразу сказать, что делает автомат, и убедиться, что он соответствует ТЗ. А если задание поменяется, граф будет достаточно просто изменить. Например, если добавляется ещё одна система счисления, нужно просто нарисовать соответствующий автоматик и присоединить его к начальному и допускающему состояниям исходного автомата ε-переходами.
Выполняющий аналогичную задачу ДКА приведён на рисунке 9 (что за цифры под состояниями – разберёмся позже, пока не обращайте внимания), он тоже не слишком сложен, более того, в данном случае даже получилось меньше состояний (а вот переходов больше, 78 против 60). Но сравните: насколько ДКА более запутан! Попробуйте, глядя на него, понять, что делает этот автомат, проверить, правильно ли он это делает, попробуйте добавить или убрать систему счисления, ещё как-нибудь изменить ТЗ…
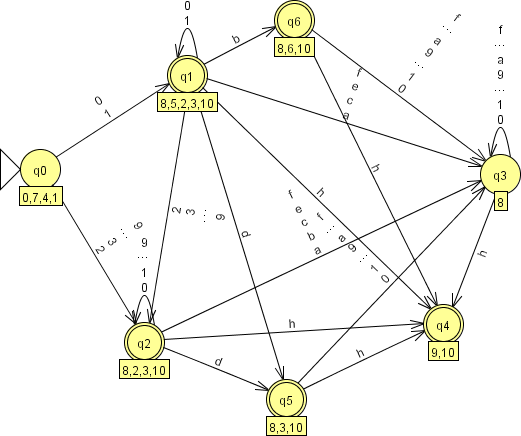
Рисунок 9. ДКА, распознающий числа в ассемблерном формате.
| ПРИМЕЧАНИЕ Помимо прочего, это ещё и не совсем правильный ДКА. В «воистину правильном» ДКА из каждого состояния есть переход по каждому символу входного алфавита, определением для ДКА не предусмотрено ситуации пустого множества состояний и «засыхания ветки вычислений». Поэтому для полного соответствия нужно добавить в автомат ещё одно состояние, в которое должны сходиться все переходы по «непредусмотренным» символам, а выхода из этого состояния не будет – по любому символу следует переход в себя. Иногда такие состояния называют «дьявольскими». |
В общем, мораль такая: с точки зрения проектирования конечных автоматов, ε-НКА – язык более высокого уровня, чем ДКА. Вычислительные возможности ε-НКА, просто НКА и ДКА совпадают – для любого ε-НКА теоретически можно построить ДКА, описывающий тот же язык (этим мы скоро займёмся), но проектировать ε-НКА гораздо, гораздо проще и удобнее.
На детерминированном компьютере проще всего реализовывать НКА, основываясь на его определении. То есть, хранить множество текущих состояний, а при обработке очередного входного символа, переходить из каждого состояния в соответствующее множество и объединять результаты.
Примерно так:
Обработка входного символа:
Set<State> tmp = new Set<State>(); // Создаём пустое множествоforeach (State s in current) { // Объединяем результаты всех переходов tmp += table[new Key(s, input)]; } // Сохраняем результат current = tmp; |
На первый взгляд, количество операций, необходимое для обработки одного символа можно оценить как O(M), где M – количество состояний автомата. Но эта оценка верна, только если вам удастся реализовать объединение множеств за константное время, не зависящее ни от размера первого множества, ни от размера второго.
Типичная сложность реализации объединения множеств линейно зависит от размера второго множества. Поскольку оценить мы его можем только как O(M), в результате сложность обработки одного символа – O(M2), обработка строки длиной N – O(N*M2).
Можно переписать код, например, так:
SetsUnion<State> tmp = new SetsUnion<State>(); // Создаём объединение множествforeach (State s in current) { // Объединяем результаты всех переходов// Операция + выполняется за константное время,// она просто добавляет множество в список tmp += table[new Key(s, input)]; } // Сохраняем результат, при этом объединяем все множества в одно // Если не объединять, будут сложности с итерацией по множеству current = tmp.normalize(); |
Но и в этом случае O(M2) никуда не уходит, просто прячется внутри метода normalize.
Правда, это, конечно, оценка худшего случая – если все состояния соединены друг с другом всеми возможными переходами, в среднем всё будет не так печально.
При желании таким же несложным способом можно реализовать и ε-НКА – нужно перед началом обработки данных и после обработки каждого символа подавать на вход автомату ε, пока множество состояний не перестанет изменяться. Примерно так:
for (;;)
{
Set<State> tmp = new Set<State>(); // Создаём пустое множествоforeach (State s in current)
{
// Объединяем результаты всех переходов по эпсилону
tmp += table[new Key(s, empty_input)];
}
if (current == tmp)
{
// Ничего не поменялось – ура, выходимbreak;
}
// Сохраняем результат
current = tmp;
}
|
Это ужасающе неэффективно, но зато работает.
Немного подумав, можно вспомнить про формальное определение ε-НКА через ε-замыкания, и сообразить, что множество eclose(qi) – фиксировано, и его нужно вычислить только один раз, причём до начала работы автомата.
В результате, получаем вот такой код:
Set<State> tmp = new Set<State>(); // Создаём пустое множествоforeach (State s in current) { // Объединяем замыкания всех текущих состояний tmp += closingsTable[new Key(s)]; } // Сохраняем результат current = tmp; |
Этот кусок тоже имеет сложность O(M2).
Рассмотрим произвольный НКА с тремя состояниями – q0, q1, q2.
Независимо от своей внутренней структуры, в каждый конкретный момент этот НКА может находиться в одном из следующих множеств состояний:
И всё, других вариантов нет. Причём переход между множествами состояний чётко детерминирован – это просто объединение значений функции перехода для каждого из состояний, и сами значения и их объединения тоже находятся в этом списке.
Обобщая наблюдения до произвольного НКА с любым количеством состояний, мы можем определить следующий ДКА:
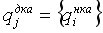
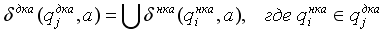
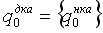
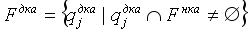
Идея преобразования основана на том, что множество подмножеств конечного множества состояний – конечно, то есть, как бы НКА не крутился, он всегда находится в одном из конечного множества состояний.
| ПРИМЕЧАНИЕ Если мысль о том, что множества состояний одного автомата являются состояниями другого автомата, пока что плохо влезает в вашу голову, можно представить то же самое менее абстрактно. Для НКА с тремя состояниями, обозначим состояния ДКА следующими строчками: * -x- * -q0- * -q1- * -q2- * -q0-q1- * -q0-q2- * -q1-q2- * -q0-q1-q2- Назначим среди этих состояний правильное начальное (оно должно соответствовать начальному состоянию НКА) и допускающие, нарисуем таблицу для функции переходов, получим ДКА. Для НКА с большим количеством состояний – по аналогии. |
С использованием индукции достаточно просто доказывается, что сконструированный ДКА описывает тот же язык (допускает точно те же цепочки символов), что и исходный НКА. Эта задача оставляется читателю в качестве упражнения :)
| СОВЕТ Индукционное предположение – в процессе обработки цепочки ДКА всегда находится в состоянии, соответствующем текущему множеству состояний НКА. База очевидна, для доказательства индукционного перехода нужно посмотреть на определение НКА и сравнить алгоритм вычисления следующего множества состояний с алгоритмом работы функции перехода нашего ДКА. А после всего этого сравнить, в каких случаях автоматы допускают цепочки. |
Конструирование ДКА, соответствующего заданному ε-НКА, немного отличается – нужно в нескольких местах заменить слова «состояние qi» на «ε-замыкание состояния qi». Вот эти места:
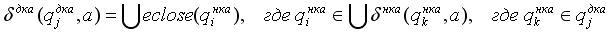
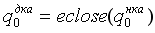
Доказательство идентичности описываемых автоматами языков аналогично доказательству для обычного НКА.
| ПРИМЕЧАНИЕ Таким образом, можно считать доказанным, что любой язык, описываемый ε-НКА, может быть описан обычным ДКА. А поскольку обратное очевидно (ДКА это просто частный случай ε-НКА), вычислительная мощность ДКА и ε-НКА совпадают. Просто хотелось отдельно отметить этот важный теоретический результат :) |
Для начала оценим количество состояний «теоретического» ДКА. Если НКА имеет M состояний, то состояниями ДКА будут все подмножества множества {q0, … qM-1}. Поскольку каждое из qi может входить или не входить в подмножество, мы получаем 2M состояний ДКА.
Такое количество состояний немного пугает, но, к счастью, часто подавляющее большинство состояний оказывается недостижимым (то есть, не существует последовательности переходов, которая приводит автомат в такое состояние из начального), поэтому их можно просто отбросить, и это никак не повлияет на описываемый ДКА язык.
Но часто – не значит всегда. Пример НКА, ДКА которого будет содержать 2M-1 состояний, приведён на рисунке 10. Вставляя «в хвост» НКА дополнительные состояния, можно неограниченно увеличивать количество состояний ДКА.
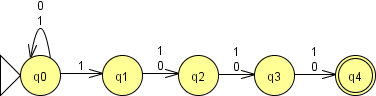
Рисунок 10. Неудачный НКА.
Возможны два подхода:
Мы пойдём вторым путём. Основная идея алгоритма:
Генерация ДКА:
// Добавляем начальное состояние в список новых
newStates.add(eclose(q0));
while (!newStates.empty())
{
// Извлекаем очередное новое состояние списка
MultiState tmp = newStates.popfront();
if (dfaStates.Contain(tmp))
{
// Оно уже есть в списке достижимыхcontinue;
}
// Это новое состояние, ещё не рассмотренное
dfaStates.add(tmp);
foreach (Symbol a in inputSymbols)
{
// Для каждого входного символа генерируем новое состояние
MultiState newTmp = tmp.transit(a).eclose();
// добавляем его в список «новых» состояний
newStates.add(newTmp);
// и устанавливаем связь в таблице переходов ДКА
dfaTransitTable.add(new Key(tmp, a), newTmp);
}
}
|
Работа ДКА:
// Сохраняем результат
current = dfaTransitTable[new Key(current, input)];
|
Оценка алгоритма генерации ДКА неутешительна. Количество операций линейно зависит от количества состояний ДКА, а верхняя оценка для них – 2M. В среднем будет получше, но тоже ничего хорошего – генерация новых состояний, то есть внутренняя часть цикла, это O(M2*S) операций (где S – количество символов).
Но зато, после того как ДКА сгенерирован, он обрабатывает любой символ за константное время, а строчку длиной N – за O(N).
.. а дальше? .. Пластилиновая ворона
Возможно (я на это надеюсь!), вам кажется, что всё описано недостаточно строго, или же что описано ужасающе мало. Этих и многих других недостатков лишена замечательная книжка «Введение в теорию автоматов, языков и вычислений», авторы Джон Хопкрофт, Раджив Мотвани, Джеффри Ульман (издательство Вильямс, 2002). Очень рекомендую, правда, вряд ли вы её найдёте в магазинах, разве что на русском выпустят третье издание.
Значительно проще найти книгу «Классика программирования: алгоритмы, языки, автоматы, компиляторы», Мозговой М.В., Наука и Техника, 2006. Тоже хорошая книжка, она менее фундаментальна и строга, ближе к программированию, и содержит куски кода на C#.
Ну а играть с автоматами проще всего в программе JFLAP, которая уже упоминалась выше.
 Оценка 720
[+1/-0] Оценка 720
[+1/-0]
  Оценить Оценить       
|